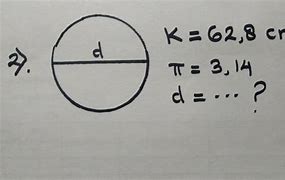
Rumus Mencari Diameter Lingkaran Jika Diketahui Kelilingnya

Rumus Titik Pusat Lingkaran

Kalau nyari jari-jari lingkaran, mungkin elo udah tau rumus r = d : 2. Tapi, gimana sih, cara mencari titik pusat lingkaran?

Salah satu cara mencari titik pusat lingkaran yaitu menggunakan rumus. Kalau di kehidupan sehari-hari, elo bisa banget menggunakan rumus di bawah ini buat nyari titik pusat lingkaran di ring basket.

Tunggu, deh. Buat apa gue nyari titik pusat lingkaran yang ada di ring basket? Eits, ini dia menariknya!

Kalau elo main basket dan tahu angka tepat dari titik pusat lingkarannya, elo bisa lebih hati-hati saat melempar bola ke dalam ring supaya bisa masuk dengan tepat.

Nah, ini rumus yang bisa elo pakai buat mencari titik pusat lingkaran.

Selain rumus di atas, sebenarnya cara mencari titik pusat lingkaran ini beragam banget, lho. Biasanya, bakal diketahui persamaan lingkaran dulu, nih. Terus, elo bisa cari titik pusat lingkaran melalui koordinat.

Misalnya, diketahui persamaan lingkaran (x-1)² + (y-2)². Nah, elo jadi langsung tahu koordinat x di angka 1. Sedangkan koordinat y di angka 2. Itu dia rumus gampangnya kalau elo mau mencari titik pusat lingkaran.

Buat cari tahu titik koordinat kayak di atas, elo juga bisa menggunakan rumus persamaan kuadrat, nih. Kayak gimana rumusnya? Elo bisa cari tahu di artikel Rumus Persamaan Kuadrat dan Akar-Akarnya, ya.

Baca Juga: Rumus Persamaan Lingkaran dan Contoh Soal – Materi Matematika Kelas 11

Contoh Soal Menentukan Titik Pusat Lingkaran

Sejauh ini, gue harap elo udah paham sama materi titik pusat lingkaran, ya. Supaya pemahaman elo semakin mendalam, gimana kalau kita adain kuis?

Yap! Gue punya tiga contoh soal buat menentukan titik pusat lingkaran, nih. Coba elo asah kemampuan elo tentang materi hari ini dengan mengerjakan ketiga soal di bawah ini, ya. Semangat!

Tentukan persamaan umum lingkaran yang melalui titik pusat lingkaran P (-3, 7) dan melalui titik Q (-9, -1).

A. (x+3)² + (y-7)² = 100

B. (x-3)² + (y-7)² = 100

C. (x+3)² + (y+7)² = 100

D. (x-3)² – (y-7)² = 100

Ingat bahwa persamaan umum lingkaran berbentuk

Dengan merupakan titik pusat lingkaran dan (y,p) merupakan titik yang dilalui. Maka dari itu, untuk lingkaran yang melalui titik pusat lingkaran P (-3, 7) dan melalui titik Q (-9, -1), dapat kita tentukan jari-jarinya terlebih dahulu, yaitu:

(-9 – (-3))² + (-1 – 7)² = r²

36 + 64 = 100, dengan demikian r² = 100

Sehingga, persamaan umum lingkarannya adalah (x + 3)² + (y-7)² = 100

Jadi, jawaban yang paling tepat yaitu A.

Diketahui persamaan standar lingkaran yaitu x² + y² – 12x + 5y = 20. Tentukan jari-jari dari lingkaran tersebut!

x² + y² – 12x + 5y = 20 merupakan persamaan standar lingkaran.

Dari (1) diperoleh dan , sehingga:

Dari persamaan (1) diketahui bahwa , maka:

Jadi, jawaban yang paling tepat yaitu A.

Diketahui persamaan standar lingkaran yaitu . Tentukan titik pusat lingkaran tersebut!

Untuk persamaan lingkaran yang berbentuk , maka titik pusatnya yaitu A = -12, B=-10. Sehingga:

Jadi, jawaban yang paling tepat yaitu B.

Gimana, materi pembelajaran kita hari ini? Nggak susah, kan? Mungkin, gue bisa highlight satu hal buat elo. Kalau elo mau mencari titik pusat lingkaran, ingat aja buat nyari titik koordinatnya dulu, ya.

Kalau koordinatnya udah ketemu, elo bisa nerusin hasil akhirnya dengan lebih mudah. Nah, dari ketiga contoh soal di atas … siapa yang jawabannya benar semua, nih?

Oh iya, kalau elo merasa tiga soal di atas masih kurang buat ngebantu elo belajar tentang titik pusat, tenang aja! Zenius punya puluhan latihan soal buat elo persiapan try out, lho.

Lumayan banget nih, bisa sambil mengasah kemampuan elo mengerjakan soal-soal nantinya. Yuk, langsung aja klik link di bawah ini buat ikutan latihan soalnya, ya!

Latihan Try Out Bareng Zenius

Nah, itu dia pembahasan kita hari ini tentang titik pusat lingkaran. Lengkap banget, kan? Mulai dari pengertian, rumus, garis singgung, sampai penjabaran dari contoh soal titik pusat lingkaran.

Kalau dari elo sendiri, gimana? Udah paham sejauh ini? Oh iya, Zenius juga punya materi matematika lainnya yang nggak kalah keren dan menarik, lho. Nah, video materi matematika di bawah ini langsung diajarin sama Sabda! Penasaran? Tonton videonya langsung, ya!

Skollamate, ketika pertama kali mendengar lingkaran, apa yang ada di pikiranmu? Hmm… Ban sepeda, kancing, jam dinding, atau pizza? Betul! Pasti kamu bisa menyebutkan banyak benda berbentuk lingkaran.

Tahukah kamu kalau benda yang kamu sebutkan tadi adalah gerbang dari sebuah konsep ilmu Matematika?

Ya! Tanpa kamu sadari, dulu kamu mengenal lingkaran hanya sebagai jenis “bentuk”. Tapi sekarang, kamu akan mengenal lingkaran lebih jauh lagi sebagai salah satu dari konsep Matematika, yaitu “bangun datar”. Menarik, kan?

Nggak sebatas bentuknya melingkar, kamu akan lebih tau serba-serbi tentang lingkaran. Kamu juga bakal ketemu rumus lingkaran yang nggak cuma ada satu. Penasaran mau pelajarin lebih lanjut? Yuk, baca di artikel ini!

Konsep Jari-Jari dan Diameter Lingkaran

Jari-jari dan diameter rupanya masih sering bikin sebagian oleng. Alias, nggak teliti saat mengerjakan soal. Akibatnya, banyak juga yang tertukar antara rumus jari-jari dan rumus diameter.

Padahal, keduanya sangat berbeda, lho, Skollamate. Memang sama-sama unsur lingkaran yang nggak jauh dari titik pusat, tapi jari-jari dan diameter memiliki definisi yang berbeda, yakni:

Nah, sudah lebih tercerahkan tentang perbedaan jari-jari dan diameter? Kalau belum, simak contoh soalnya berikut ini, deh.

Diketahui panjang diameter sebuah lingkaran adalah 20 cm, berapa jari-jarinya?

Jari-jari dari sebuah sebuah lingkaran dengan panjang diameter 20 cm adalah 10 cm.

Nah, itu dia contoh soal untuk mencari jari-jari jika yang diketahui adalah ukuran diameternya. Sekarang, coba kita balik dengan contoh berikut.

Diketahui panjang jari-jari sebuah lingkaran adalah 16 cm, berapa diameternya?

Diameter dari sebuah sebuah lingkaran dengan panjang jari-jari 16 cm adalah 32 cm.

Apakah sudah cukup jelas? So pasti sudah terasa menyenangkannya sampai sini, ya? Tapi, nggak cukup sampai di pembahasan jari-jari dan diameter. Ada yang makin menantang dan seru terkait rumus lingkaran lainnya, yaitu cara mencari tahu rumus keliling lingkaran dan luas lingkaran.

Pengertian Titik Pusat Lingkaran

Selain ngebahas tentang pengertiannya, gue juga mau ngasih tahu kalau ada unsur-unsur pelengkap di lingkaran. Emangnya, ada unsur-unsur apa aja, sih?

Pertama, ada yang namanya titik pusat lingkaran. Apa yang dimaksud dengan titik pusat lingkaran? Jadi, titik pusat lingkaran adalah titik yang berada di tengah lingkaran.

Terus, ada juga yang namanya diameter, nih. Apaan lagi, tuh? Nah, tali busur yang melewati titik pusat lingkaran disebut sebagai diameter. Unsur lainnya yang nggak kalah penting yaitu jari-jari lingkaran, letak titik pusat lingkaran ke garis lainnya.

Biar elo bisa paham seutuhnya, gue coba kasih gambaran dari titik pusat dan jari-jari lingkaran, ya.

Dengan gambar titik pusat lingkaran di atas, semoga elo jadi semakin mengerti unsur-unsur yang ada di dalam sebuah lingkaran, ya.

Tapi, gimana sih cara menentukan titik pusat lingkaran? Gue punya 3 tahapan yang bisa elo ikutin buat menentukan titik pusat lingkaran.

Nah, kalau elo mau nyari titik pusat lingkaran lewat gambar, bisa ikutin tiga langkah di atas, ya! Setelah tahu versi gambarnya, gue mau ngasih tahu rumusnya, nih.

Baca Juga: Contoh Soal Keliling dan Luas Lingkaran Beserta Rumusnya

Unsur-Unsur Lingkaran

Titik tetap yang menjadi pusat dari semua titik pada lingkaran, yaitu O.

Jarak dari pusat lingkaran ke setiap titik pada lingkaran, yaitu AO, OB, atau OC.

Jarak terpanjang yang menghubungkan dua titik pada lingkaran melalui pusat, yaitu AB.

Bagian dari keliling lingkaran yang terletak antara dua titik pada lingkaran, yaitu BC.

Garis yang menghubungkan dua titik pada lingkaran tanpa melewati pusat, yaitu AC.

Garis tegak lurus dari pusat lingkaran ke tali busur, yaitu OD dalam segitiga OAC.

Daerah dalam lingkaran yang dibatasi oleh busur dan tali busur.

Daerah yang dibatasi oleh dua jari-jari dan sebuah tali busur, yaitu BOC.

Cara Pengopelan & Rumus Menghitung Diameter Pulley di Mesin Diesel

Sebelum melakukan pengopelan terlebih dahulu harus diperhatikan hubungan antara tenaga mesin penggerak dan tenaga yang diperlukan oleh mesin kerja, sehingga dalam pengopelan akan mendapatkan hasil yang baik.

L untuk V pulley sekitar 500 – 800 mm

L untuk F pulley 3 – 4 m

Rumus Keliling Lingkaran

Sebelum cas-cis-cus langsung menghitung rumus, ketahui dulu mengenai apa itu keliling.

Keliling atau yang disimbolkan dengan huruf “K” adalah panjang seluruh garis batas lingkaran.

Rumus untuk menghitung keliling lingkaran yaitu sebagai berikut:

Jika sebuah lingkaran diketahui jari-jarinya, pakailah rumus K=2.π.r. Namun, jika sebuah lingkaran diketahui diameternya, pakailah rumus K=π.d.

Selanjutnya, ada juga unsur lingkaran yang bernama “luas” (L), tidak lain yakni jumlah daerah yang dilingkupi oleh lingkaran.

Rumus untuk menghitung luas lingkaran adalah:

Contoh Soal dan Pembahasan

Setelah tahu rumus-rumus lingkaran, inilah saatnya mengaplikasikan rumus tersebut ke dalam soal. Coba jawab soal tanpa scroll jawabannya, ya! Yuk, bersiap coret-coret dan simak contoh soalnya di bawah ini!

Sebuah lingkaran memiliki jari-jari 7 cm. Hitung keliling dan luas lingkaran tersebut. Gunakan π = 22/7.

Maka, keliling lingkaran tersebut adalah 44 cm dan luasnya 154 cm².

Sebuah lingkaran memiliki diameter 14 cm. Hitung keliling dan luas lingkaran tersebut. Gunakan π = 3,14.

L = 153,86 cm² atau 154 cm²

Maka, keliling lingkaran tersebut adalah 43,96 cm dan luas lingkarannya adalah 152,86 cm².

Sebuah lingkaran memiliki keliling 31,4 cm. Hitung jari-jari dan luas lingkaran tersebut. Gunakan π = 3,14.

Maka, jari-jari lingkaran tersebut adalah 5 cm dan luas lingkarannya adalah 78,5 cm².

Itu dia seluk-beluk perihal bangun datar bernama lingkaran, yang wujudnya kerap mengingatkan pada bola, uang koin, tutup botol, dan masih banyak benda-benda familiar di sekitar kita.

Nah, buat Skollamate yang ingin memperkaya ilmu Matematika dengan cara yang menyenangkan, kamu bisa menyimak pembahasannya lebih lanjut di aplikasi Skolla. Nggak cuma soal lingkaran dan matematika, tapi ada banyak materi lainnya yang bisa kamu pelajari di sana. Cek aplikasi Skolla untuk mulai belajar!

Contoh Soal Perhitungan Keliling Lingkaran

Melansir smpn3payakumbuh.sch.id, berikut contoh soal dan pembahasan keliling lingkaran:

Hitunglah keliling lingkaran yang mempunyai diameter 15 cm dengan π = 3,14.

Keliling = πd = 3,14 x 15 cm = 47,1 cm.

Hitunglah diameter lingkaran yang mempunyai keliling 25,12 cm dan π = 3,14.

Jadi, diameter lingkaran tersebut adalah 8 cm.

Tentukan keliling lingkaran yang berdiameter 21 cm dan π = 22/7.

Keliling = πd = 22/7 x 21 cm = 22 x 3 cm = 66 cm.

Tentukan keliling lingkaran yang berdiameter 35 cm dan π = 22/7.

Keliling = πd = 22/7 x 35 cm = 22 x 5 cm = 110 cm.

Tentukan keliling lingkaran yang berdiameter 49 cm dan π = 22/7.

Keliling = πd = 22/7 x 49 cm = 22 x 7 cm = 154 cm.

Tentukan keliling lingkaran yang berdiameter 38,5 cm dan π = 22/7/

Keliling = πd = 22/7 x 38,5 cm = 22 x 5,5 cm = 121 cm.

Tentukan keliling lingkaran yang panjang jari-jarinya 10 cm dan π = 3,14.

Keliling = 2πr = 2 x 3,14 x 10 cm = 62,8 cm.

Tentukan keliling lingkaran yang panjang jari-jarinya 15 cm dan π = 3,14.

Keliling = 2πr = 2 x 3,14 x 15 cm = 94,2 cm.

Tentukan keliling lingkaran yang panjang jari-jarinya 36 cm dan π = 3,14.

Keliling = 2πr = 2 x 3,14 x 36 cm = 226,08 cm.

Tentukan keliling lingkaran yang panjang jari-jarinya 15,5 cm dan π = 3,14.

Keliling = 2πr = 2 x 3,14 x 15,5 cm = 97,34 cm.

Diameter mata uang koin lima ratus rupiah adalah 15 mm. Hitunglah kelilingnya.

Keliling = 2πr = 2 x 3,14 x 15 mm = 94,2 mm.

Diameter sebuah roda mobil adalah 42 cm. Hitunglah keliling roda tersebut.

Keliling = πd = 22/7 x 42 cm = 22 x 6 cm = 132 cm.

Diameter lingkaran adalah sebarang ruas garis lurus yang melalui pusat lingkaran dan titik akhirnya ada pada keliling lingkaran. Titik-titik akhir diameter yang diberikan adalah dan . Titik pusat lingkaran adalah pusat diameter, yang merupakan titik tengah antara dan . Dalam hal ini titik tengahnya adalah .

Suatu percobaan dapat dilakukan untuk menentukan pusat lingkaran tanpa menggunakan alat khusus. Bahkan tidak perlu menggunakan jangka sebagaimana biasanya menggambar lingkaran, tetapi cukup menggunakan benda datar apa saja yang mempunyai sudut siku-siku yang ada di sekitar anda. Misalnya kertas. Berikut cara menentuka pusat lingkaran, pertama melukis diameter-diameternya, kemudian menentukan perpotongan kedua diameter itu.

Penjelasan teknik : Jika dua tali busur bertemu di suatu titik pada keliling lingkaran, dan kedua tali busur itu membentuk sudut siku-siku pada titik tadi, maka garis di hadapan sudut siku-siku itu pastilah garis pelurus () yang tidak lain adalah diameter lingkaran. Bila dua diameter berpotongan, maka perpotongan itulah merupakan pusat lingkaran.

Apa makanan yang paling elo suka? Kalau gue, bakso. Jujur aja, gue hampir selalu 100% tergoda buat beli bakso kalau si abang bakso lewat depan rumah. Pasti gue langsung lari ke depan buat pesen bakso. Eits, nggak lupa juga minta pakai sambal yang pedesnya nampol.

Duh, ngebayangin semangkuk bakso malah bikin gue laper, deh. Tapi, gue ngomongin bakso bukan semata-mata mau bikin elo kelaperan, ya. Terus, kenapa gue bahas bakso? Soalnya, materi kita kali ini berkaitan sama makanan tersebut.

Bukan, gue bukan mau ngasih tahu elo tutorial membuat bakso di rumah. Tapi, gue mau ngajak elo ngebahas lingkaran. Tunggu, deh. Emang apa hubungannya lingkaran sama bakso?

Jadi, bakso ini merupakan sebuah contoh lingkaran yang bersifat tiga dimensi. Kurang lebih, sama kayak bola.

Nah, kali ini, gue mau ngajak elo buat menyelami materi tentang lingkaran. Spesifiknya, soal titik pusat lingkaran. Apa aja yang bakal gue bahas? Lengkap, deh! Mulai dari pengertian titik pusat lingkaran, sampai penjabaran dari setiap contoh.

Yuk, temenin gue belajar tentang lingkaran di sini, ya!

Sebelum gue bahas lebih jauh, coba kita kenalan sama lingkaran dulu, yuk! Sebenarnya, lingkaran itu apa, sih? Iya, gue tahu kalau lingkaran ini merupakan sebuah bentuk.

Mungkin elo nggak asing sama koin sebesar Rp500 yang bentuknya lingkaran. Tapi, pengertian lingkaran itu nggak sesimpel bentuk koin yang biasa elo pakai buat beli cilok, ya.

Jadi, lingkaran dalam matematika ini didefinisikan sebagai kumpulan titik–titik yang berbentuk lingkaran dan berjarak sama terhadap satu titik di tengah.

Nah, kalau lingkarannya berbentuk dua dimensi, biasanya disebut sebagai lingkaran biasa. Tapi, kayak yang gue jelasin di awal, nih. Ada lingkaran yang bersifat tiga dimensi. Bisa jadi bola basket, futsal, bowling, atau makanan kayak bakso. Sampai sini paham, ya?

Gue sempat ngejelasin di atas kalau lingkaran ini merupakan kumpulan titik-titik, kan? Hal ini menyebabkan adanya persamaan lingkaran. Simpelnya, persamaan lingkaran ini tuh ngejelasin hubungan antara kumpulan titik-titik dari x sama y.

Psst … soal tentang persamaan lingkaran ini sering muncul di try out, lho. Tapi, tenang! Gue punya pembahasan lengkapnya yang bisa elo lihat di Rumus Persamaan Lingkaran dan Contoh Soal – Materi Matematika Kelas 11.